Simple IMU simulator

Posted

Contents

Let’s build a simple IMU simulator.

I want to have a simple testing framework doing this:

flowchart LR
    A[Reference Attitude] --> B[IMU Data]
    B --> C[Estimate Attitude]
    A --> D
    C --> D[Test accuracy]

Why not use existing datasets?

There are great datasets that include measured attitudes and recorded IMU data. However, there are many problems with it:

… among many others.

What I want is, basically, the opposite of the attitude estimator. I want to generate synthetic IMU data from a given set of attitudes.

flowchart LR
    A@{shape: lean-r, label: "Reference<br/>Attitude"} --> GenIMU[IMU Simulator]
    B@{shape: doc, label: "Sensors'<br/>configurations"} --> GenIMU
    C@{shape: doc, label: "Reference<br/>World<br/>Models"} --> GenIMU
    subgraph Generated IMU Data
        S1@{ shape: doc, label: "Accelerometer" }
        S2@{ shape: doc, label: "Gyroscope" }
        S3@{ shape: doc, label: "Magnetometer" }
    end
    GenIMU --> S1
    GenIMU --> S2
    GenIMU --> S3

Synthetic IMU data using AI is a compelling option. Unsurprisingly, there are packages built on the idea of generating sensor data from a given set of attitudes.

But these methods are constructed with, in my opinion, an unecessary complexity using NNs. I don’t fall in the frenzy of using NNs for everything. We can do better.

So, our simple IMU data generator is based on basic rules:

Before anything, let’s explore what our sensors actually measure. If you already know it, skip the next section and jump straight to the implementation.

Reference Frames

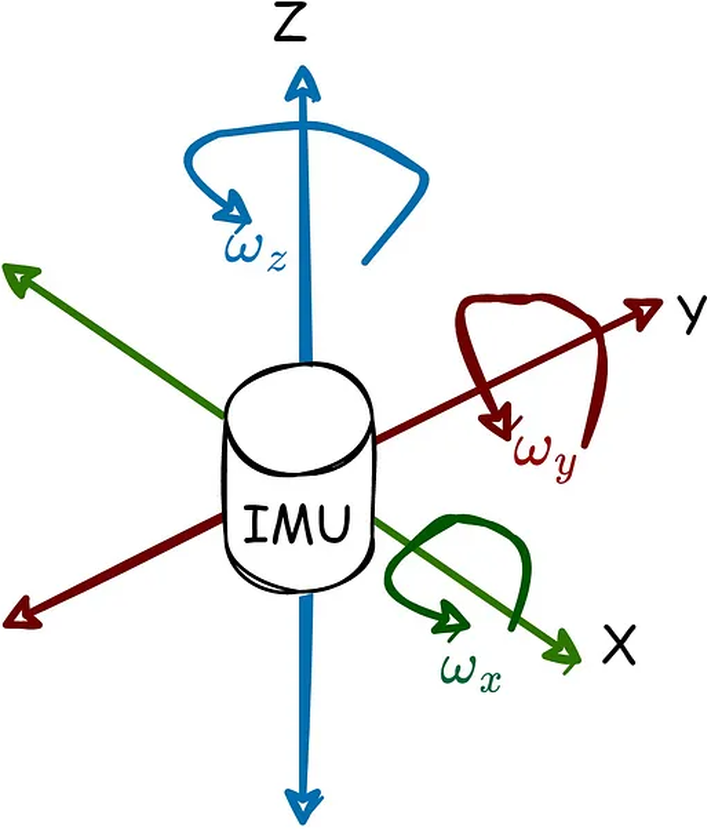
A gyroscope measures the angular velocity in the local frame of the sensor. You can consider it as a simple difference between orientations, during a certain period of time. Its reference is the previous position.

$$\boldsymbol{\omega} = \theta_{t} - \theta_{t-1}$$

where \(\boldsymbol{\omega}\) is the angular velocity in rad/s, \(\theta_{t}\) is the orientation at time \(t\), and \(\theta_{t-1}\) is the previous orientation at time \(t-1\).

But with the accelerometer and the magnetometer we use different references if we want to estimate the orientation of the sensor.

Whereas for the accelerometer we use Earth’s gravitational acceleration, for the magnetometer we would use the Geomagnetic field.

We normally use both these references when we try to estimate a rotation \(\mathbf{R}\) by solving Wahba’s Problem. The most wide-spread method to estimate an orientation.

In Wahba’s problem, we need to minimize the error between a given set of reference frames \(\mathbf{v}\) and their corresponding measurements \(\mathbf{w}\), after the have been aligned through the rotation matrix \(\mathbf{R}\). The cost function looks like this:

$$J(\mathbf{R}) = \frac{1}{2}\sum_{k=1}^{N} \|\mathbf{w}_k - \mathbf{Rv}_k\|^2 $$

for \(N\geq 2\) . Normally a set of weights are also considered, but in this case we can ommit them to simplify the model.

In this post I will assume we are also using the NED (North-East-Down) reference frame. That is the X-axis points to the geomagnetic North, the Y-axis points to the Orient, and the Z-axis points to the center of the planet.

Earth’s Gravity

This is the simplest model. To represent the gravitational acceleration with a three-dimensional vector we assume that it will always act towards the center of the planet.

That means only the Z-axis will describe the full gravitational acceleration, while the X- and Y-axis remain equal to zero:

$$\mathbf{g} = \begin{bmatrix} 0 \\ 0 \\ -g \end{bmatrix}$$

where \(g\approx 9.81 \frac{m}{s^2}\) is the gravitational acceleration.

Notice in this case we observe the global frame. Thus, the gravitational force is negative in the Z-axis.

gravity in global frame

In reality, the gravitational acceleration changes depending on the position of the device above Earth’s surface. At the poles is different than at the Equator. For that, a handy function included in ahrs can be used.

In the following example I use the geographical coordinates of Munich, Germany, where I reside.

import ahrs
# 48.137° N, and 519 m above sea level --> g = 9.807425
g = ahrs.utils.WGS().normal_gravity(48.1372, 519.0)

See the documentation of WGS for a thorough explanation of this function.

Earth’s Magnetic Field

The magnetic field of the planet is the main referene for the magnetic sensors. It is also defined in 3d aloing the X-, Y-, and Z-axis.

$$\mathbf{m} = \begin{bmatrix} m_x \\ m_y \\ m_z \end{bmatrix}$$

However, this model is more difficult to define. The magnetic field changes continually, because the ferrous material in the planet’s core is in constant motion, which reshapes its magnetic field.

The World Magnetic Model (WMM) had to be implemented using spherical harmonics for this case, and the coefficients of the model are updated every 5 years.

But we don’t have to do all that now, as the ahrs has the WMM already implemented, and we just need to build a WMM object with the geographical coordinates:

wmm = ahrs.utils.WMM(latitude=48.1372, longitude=11.5755, height=0.519) # Munich, Germany with height as km

This will estimate all magnetic elements at the given geographical point and store them as a dictionary in the attribute magnetic_elements. Alternatively, it also stores them as properties of the class.

Because we just need the magnetic intensities against the X-, Y-, and Z-axis, we could retrieve these valuesdirectly:

mag_reference = wmm.geodetic_vector # np.array([21017.71797873, 1574.05225072, 43968.18299136])

And now we have Munich’s local magnetic field in an array called mag_reference.

These two elements (gravity and magnetic field) will be, along the angular change, the main references that we are going to use to create our IMU simulator.

Sensors

Nowadays to estimate the orientation using portable low-cost sensors we use two main type of MEMs:

When using inertial sensors, we talk about an Inertial Measurement Unit (IMU). Adding a Magnetometer (Compass) it becomes a MARG (Magnetic, Angular Rate, Gravity) architecture.

In this post I will refer to both types as IMU, although it is technically incorrect. Most people are more familiar calling them IMU.

Sometimes you will see the terms 6-axis and 9-axis sensors. The first one refers to the IMU, and the second one to the MARG.

Inertial Sensors

Inertial sensors are called like that, because they take advantage of a resonating mass and its inertial properties within a frame.

When the sensor is not moving, the capacitance between semiconductive strips inside it will remain steady.

If the sensor moves, the capacitance will change because the distance between the strips has changed.

This difference in capacitance is measured and from it the applied force is estimated.

The accelerometer measures the linear force applied to it in a particular direction. If we put three of them orthogonally, we can measure the force in any direction in a three-dimensional space.

We define the accelerometer frame as equal the local frame of the sensor.

$$^l\mathbf{acc} = \begin{bmatrix}^la_x \\ ^la_y \\ ^la_z \end{bmatrix}$$

When trying to measure Earth’s gravity, we are tempted to think that an accelerometer would measure the force of gravity, but that is partially true.

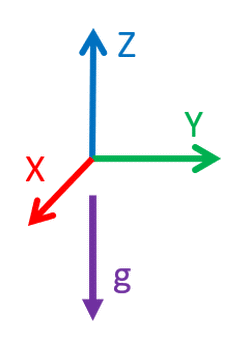
Imagine you hold the accelerometer on your hand. The force of gravity will pull the sensor downwards towards the center of the planet, but the force of your hand pushes the sensor upwards, keeping the sensor the same position.

The sensor measures the force of your hand counteracting the effect gravity.

If we read the measurements of the accelerometer, we will get a set of values like this:

$$\mathrm{accelerometer}=\begin{bmatrix} 0 \\ 0 \\ 9.81 \end{bmatrix}$$

The X- and Y-axis will measure zero, because there is no force acting upon them. The Z-axis will measure the force of our hand (yellow) counteracting the force of gravity (purple.)

Notice the value is positive because is colinear with the Z-axis of the accelerometer and has the same direction pointing upwards.

Now, if you let the sensor fall, the accelerometer will measure values close to zero, because there are no forces counteracting the gravitational acceleration.

That’s actually a simple technique some computers use to detect if they are falling, and they shut down to prevent damage.

This principle works for both accelerometers and gyroscopes. The latter ones are built in a way that it can calculate the applied angular force, instead of linear.

Magnetic Sensors

Magnetic MEMS are mostly built considering the Hall effect.

Hall effect sensors measure the changing voltage across an electrical conductor when a magnetic field is applied perpendicular to the current.

Perfect IMUs

With these basic principles we can start building our IMU generator.

Using Recorded Data

Let’s take a recording of the trusted RepoIMU dataset, and compare it with the signals generated by our IMU simulator.

This dataset has good advantages:

However, it also has some drawbacks:

The data was recorded at the Human Motion Laboratory of the Polish-Japanese Academy of Information Technology in Bytom, Poland, whose coordinates are 50.35363 N 18.9148285 E, and elevation is equal to 280 m.

As the article was published in September 2016, we can assume the recordings were made in early 2016.

With this information we can compute the magnetic reference vector with ahrs:

wmm = ahrs.utils.WMM(date=2016.0, latitude=50.35363, longitude=18.9148285, height=0.28)
magnetic_reference = np.array([wmm.X, wmm.Y, wmm.Z])

However, the creators of the dataset mention that the magnetic field is estimated with the simplified NED model:

$$\mathbf{m} = \begin{bmatrix} \cos\phi \\ 0 \\ \sin\phi \end{bmatrix}$$

where \(\phi=66°\) is the geographical latitude angle of the laboratory.

Let’s take their word and define the referencial magnetic field vector as:

$$ \mathbf{m} = \begin{bmatrix} \cos(66°) \\ 0 \\ \sin(66°) \end{bmatrix} = \begin{bmatrix} 0.4067 \\ 0 \\ 0.9135 \end{bmatrix} $$

This vector is already normalized (\(\|\mathbf{m}\|=1\)).

With it the referencial geodetic vectors become:

# Reference gravitational vector (actually force of your hand counteracting gravity)
g = 9.81        # 9.81 m/s^2
reference_gravity = np.array([0.0, 0.0, g])

# Reference magnetic vector (normalized)
angle = 66.0
reference_magnetic_vector = np.array([np.cos(np.radians(angle)), 0.0, np.sin(np.radians(angle))])

Now we load and organize a recording of the dataset:

import numpy as np

# Load data
repoimu_data = np.loadtxt("TStick_Test02_Trial2.csv",
                          dtype=float,
                          delimiter=';',
                          skiprows=2)

# Reference quaternions from VICON system
quaternions = repoimu_data[:, 1:5]

# Measured IMU sensor signals
measured_accelerometers = repoimu_data[:, 5:8]
measured_gyroscopes = repoimu_data[:, 8:11]
measured_magnetometers = -repoimu_data[:, 11:14]    # Inverted magnetic field

The measured sensor signals will be used to compare against the generated ones.

Now we generate new sensor signals using only the orientations from the dataset. Let’s first assume our sensors are perfect, and we don’t add any intrinsic nor extrinsic errors.

# Reference attitudes as quaternions
reference_quaternions = ahrs.QuaternionArray(repoimu.quaternions)
num_samples = len(reference_quaternions)

# Angular velocity in sensor frame [rad/s]
angular_velocity = reference_quaternions.angular_velocities(1/repoimu.frequency)
gyroscopes = np.vstack([angular_velocity[0], angular_velocity])

# Reference attitudes as rotation matrices
rotations = reference_quaternions.to_DCM()

# Acceleration in global frame [m/s^2]
accelerometers = np.array([rot.T @ reference_gravity for rot in rotations])

# Magnetic field in global frame (normalized)
magnetometers = np.array([rot.T @ reference_magnetic_vector for rot in rotations])

Let’s compare the generated gyroscopes against the measured ones:

… the Accelerometers:

… and, finally, the most interesting one, the Magnetometers:

Our generated data is very close to the measured data. We can call it a success.

There are some things we have to consider:

A disadvantage is the big sensitivity to any type of magnetic force. For example, any electric device (even simple cables) generate a magnetic field when a current flows through them.

Those fields greatly affect the measurements when nearby, and are technically impossible to predict.

Sensor Error Model

Three-dimensional sensor configurations (measuring along X-, Y-, and Z-axis) build these sensors orthogonally inside the chips.

Nonetheless, sensors aren’t perfect, they all give you corrupted data, and this is mainly due to external factors that cannot be controlled by the user or the manufacturer, but they can be estimated and corrected.

Intrinsic Errors

There are 3 main intrinsic values, also known as deterministic errors altering the measurements:

They are called intrinsic because they are unique for each sensor, and are part of the sensor’s construction. They cannot be changed, but they can be estimated and compensated.

Extrinsic Errors

The extrinsic parameters altering the measurements are more difficult to identify, as they appear depending on the working environment of the sensors. The main ones are:

Each one of these errors has an impact in every single sensor of our device.

Some manufacturers call this confuguration a 6 degree-of-freedom (6-DOF) sensor:

When using a MARG, these sensors are advertised as 9-DOF sensors (adding 3 further degrees for the Magnetometer) or even 9-axis sensors.

Let’s build the error model step-by-step, gradually adding the values of interest.

First, let’s assume our sensors are perfect. Therefore, the sensor’s value a’ is equal to the real input a (the real physical value.)

graph LR
    A[Real<br/>input] --> B[Sensor<br/>Measurement]

Mathematically, we represent it as:

$$\mathbf{a}’ = \mathbf{a}$$

$$\begin{bmatrix} a’_x \\ a’_y \\ a’_z \end{bmatrix} = \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix}$$

The first errors we might encounter are the scaling factors of each sensor.

graph LR
    A[Real<br/>input] --> B[Scaling<br/>factor]
    B --> C[Sensor<br/>Measurement]

As mentioned before, it affects the sensors linearly and independently:

$$ \begin{array}{rcl} \mathbf{a}’ &=& \mathbf{Sa} \\ &=& \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \end{bmatrix} \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix} \\ \\ \begin{bmatrix} a’_x \\ a’_y \\ a’_z \end{bmatrix} &=& \begin{bmatrix} s_xa_x \\ s_ya_y \\ s_za_z \end{bmatrix} \end{array} $$

When the values in the diagonal of the scaling matrix \(\mathbf{S}\) are all equal to one, there is no scaling and, thus, our sensors are perfectly scaled. This never happens in reality.

The rest of the matrix remains empty (equal to zero), because those places relate the influence of each axis over the other. However, those values are very useful, because they represent the sensitivity between the axes of our sensor array.

We can estimate the orthogonality already. When those orthogonal deviations are equal to zero, we have a perfect orthogonality.

Because the orthogonality is also linearly independent, we can represent it with another matrix multiplying the input values.

graph LR
    A[Real<br/>input] --> B[Orthogonality<br/>deviations]
    B[Orthogonality<br/>deviations] --> C[Scaling<br/>factor]
    C --> D[Sensor<br/>Measurement]

$$ \begin{array}{rcl} \mathbf{a}’ &=& \mathbf{SUa} \\ &=& \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \end{bmatrix} \begin{bmatrix} 1 & u_{xy} & u_{xz} \\ u_{yx} & 1 & u_{yz} \\ u_{zx} & u_{zy} & 1 \end{bmatrix} \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix} \\ \\ \begin{bmatrix} a_x’ \\ a_y’ \\ a_z’ \end{bmatrix} &=& \begin{bmatrix} s_xa_x + s_xu_{xy}a_y + s_xu_{xz}a_z \\ s_yu_{yx}a_x + s_ya_y + s_yu_{yz}a_z \\ s_zu_{zx}a_z + s_zu_{zy}a_y + s_za_z \end{bmatrix} \end{array} $$

With a perfectly aligned sensor array this matrix would become an identity matrix \(\mathbf{I}_3\) and their multiplication would get us back to the perfect sensor assumption.

This can be further simplified to a unique linear operation:

graph LR
    A[Real<br/>input] --> B[Orthogonality<br/>and Scaling]
    B --> C[Sensor<br/>Measurement]

$$\begin{array}{rcl} \mathbf{a}' &=& \mathbf{Ma} \\ &=& \begin{bmatrix} s_x & m_{xy} & m_{xz} \\ m_{yx} & s_y & m_{yz} \\ m_{zx} & m_{zy} & s_z \end{bmatrix} \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix} \\ \\ \begin{bmatrix} a_x’ \\ a_y’ \\ a_z’ \end{bmatrix} &=& \begin{bmatrix} s_xa_x + m_{xy}a_y + m_{xz}a_z \\ m_{yx}a_x + s_ya_y + m_{yz}a_z \\ m_{zx}a_z + m_{zy}a_y + s_za_z \end{bmatrix} \end{array} $$

where the values \(m_{xy}\), \(m_{xz}\), etc., are the products of scaling factors and orthogonality deviations.

This notation can be read as the sensitivity of each axis. For example, \(m_{xy}\) is the “measurement corresponding to the X-axis, but sensed in the Y-axis.” Again, in a perfect orthogonal array, they all would be equal to zero.

Normally, we would write \(m_{xx}\) as the measurement corresponding to X-axis sensed in the X-axis, but that is clearly the scale factor \(s_x\), and we leave it unchanged.

The next value to define is the bias. The bias is an offset \(\mathbf{b}\) appearing in each sensor, which we describe as:

graph LR
    A[Real<br/>input] --> B[Orthogonality<br/>and Scaling]
    B --> C@{ shape: circle, label: " + " }
    D[Sensor<br/>Bias] --> C
    C --> E[Sensor<br/>Measurement]

$$\begin{array}{rcl} \mathbf{a}’ &=& \mathbf{Ma} + \mathbf{b} \\ &=& \begin{bmatrix} s_x & m_{xy} & m_{xz} \\ m_{yx} & s_y & m_{yz} \\ m_{zx} & m_{zy} & s_z \end{bmatrix} \begin{bmatrix} a_x \\ a_y \\ a_z \end{bmatrix} + \begin{bmatrix} b_x \\ b_y \\ b_z \end{bmatrix} \\ \begin{bmatrix} a_x’ \\ a_y’ \\ a_z’ \end{bmatrix} &=& \begin{bmatrix} s_xa_x + m_{xy}a_y + m_{xz}a_z + b_x \\ m_{yx}a_x + s_ya_y + m_{yz}a_z + b_y \\ m_{zx}a_z + m_{zy}a_y + s_za_z + b_z\end{bmatrix}\end{array}$$

Thanks to the magic of Algebra we treat the drift as a shift with homogeneous coordinates and rewrite the operation to perform a single linear operation again:

graph LR
    A[Real<br/>input] --> B[Homogeneous<br/>Vector]
    B --> C[Orthogonality,<br/>Scaling<br/>and Bias]
    C --> D[Sensor<br/>Measurement]

$$\begin{array}{rcl} \mathbf{a}’ &=& \mathbf{Ca_h} \\ &=& \begin{bmatrix} s_x & m_{xy} & m_{xz} & b_x \\ m_{yx} & s_y & m_{yz} & b_y \\ m_{zx} & m_{zy} & s_z & b_z \end{bmatrix} \begin{bmatrix} a_x \\ a_y \\ a_z \\ 1 \end{bmatrix} \\ \begin{bmatrix} a_x’ \\ a_y’ \\ a_z’ \end{bmatrix} &=& \begin{bmatrix} s_xa_x + m_{xy}a_y + m_{xz}a_z + b_x \\ m_{yx}a_x + s_ya_y + m_{yz}a_z + b_y \\ m_{zx}a_z + m_{zy}a_y + s_za_z + b_z \end{bmatrix}\end{array}$$

Finally, all sensors suffer from a random noise that is Gaussian in nature.

This cannot be corrected by a simple linear operation. The best solution is to model it as a random variable sampled from a normal distribution with mean zero and a standard deviation \(\sigma\).

$$\mathbf{e} \sim \mathcal{N}(0, \sigma^2)$$

graph LR
    A[Real<br/>input] --> B[Homogeneous<br/>Vector]
    B --> C[Orthogonality,<br/>Scaling,<br/>Bias]
    C --> D[Random<br/>Noise]
    D --> E[Sensor<br/>Measurement]

$$ \begin{array}{rcl} \mathbf{a}’ &=& \mathbf{Ca_h} + \mathbf{e} \\ &=& \begin{bmatrix} s_x & m_{xy} & m_{xz} & b_x \\ m_{yx} & s_y & m_{yz} & b_y \\ m_{zx} & m_{zy} & s_z & b_z \end{bmatrix} \begin{bmatrix} a_x \\ a_y \\ a_z \\ 1 \end{bmatrix} + \begin{bmatrix} e_x \\ e_y \\ e_z \end{bmatrix} \\ \begin{bmatrix} a_x’ \\ a_y’ \\ a_z’ \end{bmatrix} &=& \begin{bmatrix} s_xa_x + m_{xy}a_y + m_{xz}a_z + b_x + e_x \\ m_{yx}a_x + s_ya_y + m_{yz}a_z + b_y + e_y \\ m_{zx}a_z + m_{zy}a_y + s_za_z + b_z + e_z \end{bmatrix} \end{array} $$

This way, we arrive to a General Error Model for the inertial sensors using this simple linear relation of the input and output values.

The \(3\times 4\) matrix \(\mathbf{C}\) contains all unknown intrinsic parameters altering the real values, and \(\mathbf{a_h} = \begin{bmatrix}a_x & a_y & a_z & 1\end{bmatrix}^T\) is the homogeneous vector of the real values.

We could further reduce the operation to a single matrix multiplication with the last column of \(\mathbf{C}\) being the sum of the bias and the gaussian noise. But let’s keep it separated for clarity.

This is the general model we will always use to derive our sensor models.

Synthetic Orientations

We can either use pre-defined orientations or generate random ones. The first option is easier (and we did it above), but the second one is more fun.

Random orientations

ahrs has a class called Sensor that creates random orientations and generates IMU sensor signals. But let’s build it again step by step to understand the process.

First, we define the range of the Euler angles. Remember, a full rotation is \(2\pi\) radians. Defining the range as \([-\pi, \pi]\) we cover the whole range of the angles.

import numpy as np
span = [-np.pi, np.pi]

So let’s generate 1000 random samples that are uniformly distributed in this range, and would represent the Euler angles of the orientations.

rng = np.random.default_rng(42)   # Seed random number generator for reproducibility
num_samples = 1000
angles = rng.uniform(span[0], span[1], (num_samples, 3))

This will create 1000 random orientations as Euler angles. The first column will contain the roll, the second the pitch, and the third the yaw angles.

If we visualize them, we get …

a mess.

This is because the angles are not continuous. This is basically noise.

We need a more realistic motion.

Let’s take a step back. We start by defining a set of positions, where there is no motion. So, all values along each axis are equal to zero. This means, the sensor is static and aligned with the global reference frame.

angles = np.zeros((num_samples, 3))

We then define a set of random angular positions along each axis, in this case 5 different angular positions per axis.

num_positions = 5
angular_positions = [rng.uniform(span[0], span[1], num_positions) for _ in np.arange(3)]

And now we randomly distribute these positions along each axis.

for axis, positions in enumerate(angular_positions):
    indices = rng.integers(0, num_samples, num_positions)
    angles[indices, axis] = positions

Better, but still horrible. Why? Because the motion is too abrupt. It describes a system that is static, and suddenly appears in a new position for a single sample, then immediately appears back in the original position in the next sample.

We need a motion that is more continuous.

Instead of randomly distributing the angular positions, we can set them to stay constant during certain intervals.

For example, we can create an array with a range for each angular position, and then set the values of the angles at those positions.

ranges = np.sort(rng.integers(0, num_samples, 2*num_positions)).reshape((num_positions, 2))
for axis, positions in enumerate(angular_positions):
    for idx, (start, end) in enumerate(ranges):
        angles[start:end, axis] = positions[idx]

Great. Now we have 5 random positions along each axis, and they are constant during a certain interval.

This is a more acceptable motion, but it is still too abrupt. We need a smoother transition between the positions.

We can use a spline interpolation to create a smooth transition between the positions, but that means we would need to further sub-sample the data.

A more convenient option is to smooth the data using a gaussian blur. Originally applied to remove noise in digital signals, the gaussian filter will create a smooth transition between the positions, and it is easier to implement.

SciPy has a function called gaussian_filter1d that does exactly that for one-dimensional data like ours, but that means we would need to install SciPy. Let’s keep it fun, and build our own gaussian filter.

The gaussian function used for this purpose is defined as:

$$f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x)^2}{2\sigma^2}}$$

where \(\sigma\) is the standard deviation of the gaussian distribution.

The term \(\frac{1}{\sqrt{2\pi}\sigma}\) is a normalization factor that ensures the area under the curve is equal to one. This is important because we don’t want to change the magnitude of the angles.

def __gaussian_filter(in_data, window_size=50, sigma=5.0):
    x = np.linspace(-sigma*4, sigma*4, window_size)
    phi_x = np.exp(-x**2/(2.0*sigma**2))
    phi_x /= phi_x.sum()    # Normalization equivalent to the term 1/(sqrt(2*pi)*sigma)
    return np.correlate(in_data, phi_x, mode='same')

If we use this function to smooth the angles, we get …

smooth_angles = np.array([__gaussian_filter(angles[:, i], window_size=50, sigma=5.0) for i in np.arange(3)]).T

And now we can see the magnitudes of the original angles are kept, while the transitions between the positions are smoother.

We could further smooth the data by increasing the window size or the standard deviation of the gaussian function. But this is enough for now.

We have our reference orientations!

The whole process for a generator of random orientations as Euler angles is:

# Seed random number generator for reproducibility
rng = np.random.default_rng(42)

# Basic attributes
num_samples = 1000
num_positions = 5
span = [-np.pi, np.pi]  # Span of the Euler angles

# Start with no change in orientation (sensor is aligned with the global frame)
angles = np.zeros((num_samples, 3))

# Random angular positions
angular_positions = [rng.uniform(span[0], span[1], num_positions) for _ in np.arange(3)]

# Set a range for each angular position
ranges = np.sort(GENERATOR.integers(0, num_samples, 2*num_positions)).reshape((num_positions, 2))

# Distribute the angular positions
for axis, positions in enumerate(angular_positions):
    for idx, (start, end) in enumerate(ranges):
        angles[start:end, axis] = positions[idx]

# Smooth data for a better transition between positions
smooth_angles = __gaussian_filter(angles, size=40, sigma=20.0)

graph TD
    Attributes@{ shape: doc, label: "Basic<br/>Attributes"} --> Angular_Positions@{ shape: rect, label: "Random Angular<br/>Positions" }
    Angular_Positions --> Distribute@{ shape: rect, label: "Distribute<br/>Angular Positions" }
    Distribute --> Smooth@{ shape: rect, label: "Smooth Data" }
    Smooth --> ReferenceAngles@{ shape: doc, label: "Reference<br/>Euler Angles" }

IMU Sensor Signals

Now we need to generate the signals of each sensor of the IMU.

Gyroscopes

Gyroscopes measure the angular velocity of the sensor. This means, they measure the change in orientation during a certain period of time, in the sensor’s local frame.

We can calculate the angular velocity by taking the difference between the angles at two consecutive samples, and dividing it by the time between them (\(\Delta t\)).

Assuming our sampling frequency is 100 Hz, the time between samples is 0.01 seconds.

dt = 0.01
angular_velocity = np.diff(smooth_angles, axis=0)/dt

This will give us the angular velocity in radians per second. But be careful, the first sample will be lost, because we are taking the difference between. If we have N samples of angular positions, we will get N-1 samples of angular velocities.

We fix it by preprending a sample with the same value as the first one.

angular_velocity = np.vstack((angular_velocity[0], angular_velocity))

This the angular velocity measured in the local frame of the sensor around its X-, Y-, and Z-axis.

If the gyroscopes were perfect, these values would be the exact angular velocities of the sensor. But they are not, and we need to add the intrinsic errors.

We can model them as a matrix multiplication, as we did before with the general error model.

# Scaling factor
s = np.diag([1.001, 0.998, 1.002])

# Orthogonality deviations
m = np.array([[0.0, 0.0002, 0.0003], [0.0002, 0.0, 0.0002], [0.0003, 0.0002, 0.00]])

# Bias
b = np.array([0.001, 0.002, 0.003])

# General Error Model
C = np.c_[s + m, b]

These values are completely arbitrary, and they are just for demonstration. You would need to estimate them from the datasheet of your sensor, or from empirical data.

Now we can apply the error model to each sample of the angular velocity.

# Homogeneous array for the matrix multiplication
angular_velocity_homogeneous = np.c_[angular_velocity, np.ones((num_samples, 1))]
gyroscopes = (C @ angular_velocity_homogeneous.T).T

At first sight the values seem to be the same, but they are not. The intrinsic errors have been added to the angular velocities. Hover over the plot to see the values, and confirm they are different.

Now we need to add the extrinsic errors. We will use the same model as before, but we will add a random noise to the values.

The extrinsic errors are normally distributed, and they are added to the measurements as a simple additive gaussian noise:

$$\mathbf{a}’ = \mathbf{Ca} + \mathbf{n}$$

where \(\mathbf{n}\) is a random vector sampled from a normal distribution with zero mean and standard deviation \(\sigma_{\omega}\).

$$\mathbf{n} \sim \mathcal{N}(0, \sigma_{\omega}^2)$$

For this example, we set \(\sigma_{\omega}=0.5\)

std_dev = 0.5
noise = rng.standard_normal(gyroscopes.shape) * std_dev**2
gyroscopes += noise

In summary, the whole process to generate the gyroscope signals is:

# Time step = 1 / sampling frequency
dt = 0.01
angular_velocity = np.diff(smooth_angles, axis=0)/dt
angular_velocity = np.vstack([angular_velocity[0], angular_velocity])

# Scaling factor
s = np.diag([1.001, 0.998, 1.002])

# Orthogonality deviations
m = np.array([[0.0, 0.0002, 0.0003], [0.0002, 0.0, 0.0002], [0.0003, 0.0002, 0.00]])

# Bias
b = np.array([0.001, 0.002, 0.003])

# Intrinsic errors
C = np.c_[s + m, b]

# Add a column of ones to end of angular velocity array
angular_velocity_homogeneous = np.c_[angular_velocity, np.ones((num_samples, 1))]

# Apply the error model
gyroscopes = (C @ angular_velocity_homogeneous.T).T

# Add extrinsic errors
std_dev = 0.5
gyroscopes += rng.standard_normal((num_samples, 3)) * std_dev**2

graph TD
    A@{ shape: doc, label: "Random<br/>Orientations" } --> Diff@{ shape: rect, label: "Rate<br/>Change" }
    Diff --> AngVel@{ shape: lean-r, label: "Angular<br/>Velocity" }
    subgraph Intrinsic Errors
        S1@{ shape: doc, label: "Scaling<br/>Factor" }
        S2@{ shape: doc, label: "Orthogonality<br/>Deviations" }
        S3@{ shape: doc, label: "Bias" }
    end
    subgraph Extrinsic Errors
        S4@{ shape: lean-r, label: "Standard<br/>Deviation" } --> S5@{ shape: doc, label: "Gaussian<br/>noise" }
    end
    AngVel --> Add@{ shape: f-circ, label: "Addition" }
    S1 --> Add
    S2 --> Add
    S3 --> Add
    S5 --> Add
    Add --> Gyroscopes@{ shape: doc, label: "Gyroscopes" }

Accelerometers

The accelerometer measures all accelerations acting upon the sensor. In our case we are only interested in the gravitational acceleration acting upon it.

The generated angles represent the orientations of the sensor with respect to the global frame.

However, the gravitational acceleration is acting upon the sensor in the local frame, and we need to transform it to the global frame. For that we require an inverse rotation matrix to transform the gravitational acceleration from the local frame to the global frame.

This transformation is done using the rotation matrix \(\mathbf{R}\):

$$\mathbf{R} = \begin{bmatrix} \cos\theta\cos\psi & \cos\theta\sin\psi & -\sin\theta \\ \sin\phi\sin\theta\cos\psi - \cos\phi\sin\psi & \sin\phi\sin\theta\sin\psi + \cos\phi\cos\psi & \sin\phi\cos\theta \\ \cos\phi\sin\theta\cos\psi + \sin\phi\sin\psi & \cos\phi\sin\theta\sin\psi - \sin\phi\cos\psi & \cos\phi\cos\theta \end{bmatrix}$$

where \(\phi\), \(\theta\), and \(\psi\) are the roll, pitch, and yaw angles respectively.

The inverse of the rotation matrix is the transpose of the rotation matrix. This is valid for ALL matrices in SO(3):

$$\mathbf{R}^{-1} = \mathbf{R}^T$$

A simpler and faster implementation of the rotation operations can be carried out with Quaternions. The package ahrs comes to the rescue again.

We build a set of Quaternions, store them in a big array, and then transform them to rotation matrices.

from ahrs import QuaternionArray
reference_quaternions = QuaternionArray(rpy=smooth_angles)
rotations = reference_quaternions.to_DCM()

The referencial gravity vector is built with the value previously defined:

reference_gravity = np.array([0.0, 0.0, g])

Each rotation matrix will multiply the gravitational acceleration in the local frame to get the gravitational acceleration in the global frame.

accelerations = np.array([rot.T @ reference_gravity for rot in rotations])

These are the accelerations acting upon the sensor in the global frame.

As we did with the gyroscope signals, we need to add the intrinsic and extrinsic errors to the accelerations.

s = np.diag([1.001, 0.998, 1.002])      # Scaling factor
m = np.array([[0.0, 0.0002, 0.0003],    # Orthogonality deviations
              [0.0002, 0.0, 0.0002],
              [0.0003, 0.0002, 0.00]])
b = np.array([0.001, 0.002, 0.003])     # Bias

# Homogeneous array for matrix multiplication
accelerations_homogeneous = np.c_[accelerations, np.ones((num_samples, 1))]

# Add intrinsic errors
C = np.c_[s + m, b]
accelerometers = (C @ accelerations_homogeneous.T).T

# Add extrinsic errors
std_dev = 0.5
accelerometers += rng.standard_normal((num_samples, 3)) * std_dev**2

The entire process to generate the accelerometer signals is very similar to the gyroscope signals, with some minor changes at the beginning, where instead of calculating the angular velocity, we calculate the acceleration in the global frame. The errors are added the same way.

graph TD
    A@{ shape: doc, label: "Random<br/>Orientations" } --> Quats@{ shape: rect, label: "Quaternions" }
    Quats --> RotMat@{ shape: rect, label: "Rotation<br/>Matrices" }
    RotMat --> RotateAccel@{ shape: rect, label: "Rotate to<br/>global frame" }
    B@{ shape: doc, label: "Reference<br/>Gravity Vector" } --> RotateAccel
    RotateAccel --> Acc@{ shape: lean-r, label: "Accelerations in<br/>global frame" }
    subgraph Intrinsic Errors
        S1@{ shape: doc, label: "Scaling<br/>Factor" }
        S2@{ shape: doc, label: "Orthogonality<br/>Deviations" }
        S3@{ shape: doc, label: "Bias" }
    end
    subgraph Extrinsic Errors
        S4@{ shape: lean-r, label: "Standard<br/>Deviation" } --> S5@{ shape: doc, label: "Gaussian<br/>noise" }
    end
    Acc --> Add@{ shape: f-circ, label: "Addition" }
    S1 --> Add
    S2 --> Add
    S3 --> Add
    S5 --> Add
    Add --> Accelerometers@{ shape: doc, label: "Accelerometers" }

Magnetometers

And for the magnetometers, the process is the same as for the accelerometers.

  1. Transform the magnetic field from the local frame to the global frame.
  2. Add the intrinsic errors.
  3. Add the extrinsic errors.
graph TD
    A@{ shape: doc, label: "Random<br/>Orientations" } --> Quats@{ shape: rect, label: "Quaternions" }
    Quats --> RotMat@{ shape: rect, label: "Rotation<br/>Matrices" }
    RotMat --> RotateMag@{ shape: rect, label: "Rotate to<br/>global frame" }
    B@{ shape: doc, label: "Reference<br/>Geomagnetic<br/>Field Vector" } --> RotateMag
    RotateMag --> Acc@{ shape: lean-r, label: "Magnetic Flux in<br/>global frame" }
    subgraph Intrinsic Errors
        S1@{ shape: doc, label: "Scaling<br/>Factor" }
        S2@{ shape: doc, label: "Orthogonality<br/>Deviations" }
        S3@{ shape: doc, label: "Bias" }
    end
    subgraph Extrinsic Errors
        S4@{ shape: lean-r, label: "Standard<br/>Deviation" } --> S5@{ shape: doc, label: "Gaussian<br/>noise" }
    end
    Acc --> Add@{ shape: f-circ, label: "Addition" }
    S1 --> Add
    S2 --> Add
    S3 --> Add
    S5 --> Add
    Add --> Magnetometers@{ shape: doc, label: "Magnetometers" }

magnetic_field = np.array([rot.T @ mag_reference for rot in rotations])

s = np.diag([1.001, 0.998, 1.002])      # Scaling factor
m = np.array([[0.0, 0.0002, 0.0003],    # Orthogonality deviations
              [0.0002, 0.0, 0.0002],
              [0.0003, 0.0002, 0.00]])
b = np.array([0.001, 0.002, 0.003])     # Bias

# Homogeneous array for matrix multiplication
magnetic_field_homogeneous = np.c_[magnetic_field, np.ones((num_samples, 1))]

# Add intrinsic errors
C = np.c_[s + m, b]
magnetometers = (C @ magnetic_field_homogeneous.T).T

# Add extrinsic errors
std_dev = 10.0
magnetometers += rng.standard_normal((num_samples, 3)) * std_dev**2

In this case the standard deviation is set to 10.0 (empirically), because the magnetic field can reach values up to 100,000 nT along the X-, Y-, and Z-axis.

Using synthetic data to test attitude estimators

We can use the IMU simulator data to estimate the original orientation of the sensor, further testing the performance of the simulator.

Let’s now create synthetic orientations, generate sensor data, add intrinsic and extrinsic errors, and use these sensor signals to estimate the orientation of the sensor.

The reference synthetic orientations as quaternions look like this:

Now let’s use one of our favorite methods, the Madgwick Filter to estimate the orientations as quaternions using the generated IMU signals.

from ahrs.filters import Madgwick
madgwick = Madgwick(acc=accelerometers, gyr=gyroscopes, mag=magnetometers, frequency=100.0)
estimated_quaternions = ahrs.QuaternionArray(madgwick.Q)
estimated_quaternions.rotate_by(estimated_quaternions[0]*np.array([1.0, -1.0, -1.0, -1.0]), inplace=True)

The last line is a trick to align the estimated quaternions with the reference quaternions. This is because all filters assume an initial orientation coincident with the global frame, and we need to align their frames.

Plotting the estimated orientations we get:

Well, it is not precisely the same, but it is close enough.

We can also plot the differences between the estimated and the reference quaternions using the Quaternion Angle Difference.

diff_quaternions = ahrs.utils.metrics.qad(reference_quaternions, estimated_quaternions)

We see that the Madgwick Algorithm performs much better when the sensor frame goes closer to the global frame.

There might be some tuning needed for the Madgwick Filter, but the IMU simulator is working as expected.

We can play around with the intrinsic and extrinsic errors to see how they affect the estimation of the orientation.

Conclusion

In this post we have built a simple IMU simulator using the ahrs package.

We created random orientations, and generated the signals of the gyroscope, accelerometer, and magnetometer.

We have added intrinsic and extrinsic errors to the signals, and used the Madgwick Filter to estimate the orientation of the sensor to test the IMU signals.

The results are not perfect, but they are good to start. In the future we could add more sensors or physical properties to the simulator, and test it with more filters, with different algorithms, etc.

If you want to use a simple IMU simulator that implements all this and more, use the class Sensors included in the ahrs package.

import ahrs
sensor_data = ahrs.Sensors(num_samples=1000, in_degrees=False)
reference_quaternions = sensor_data.quaternions
gyroscopes = sensor_data.gyroscopes
accelerometers = sensor_data.accelerometers
magnetometers = sensor_data.magnetometers

I hope you enjoyed this post. If you have any questions or comments that could help me to improve it, please let me know.